Từ đây tới chương 2 sẽ là các bài viết về bài tập nhằm giúp các bạn hiểu hơn về những lý thuyết đã qua.
Để không quá dài, mình sẽ chỉ để khoảng từ 8-10 bài tập mỗi bài viết.

Problem-21

Tìm độ phức tạp của hàm đệ quy:

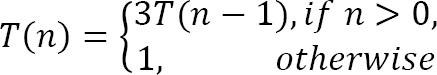
Solution: Chúng ta hãy thử giải quyết function này bằng cách substitution(thay thế):
$T ( n ) = 3 T ( n - 1 )$
$T ( n ) = 3 ( 3 T ( n - 2 ) ) = 3 ^ { 2 } T ( n - 2 )$
$T ( n ) = 3 ^ { 2 } ( 3 T ( n - 3 ) )$
...
$T ( n ) = 3 ^ { n } T ( n - n ) = 3 ^ { n } T ( 0 ) = 3 ^ { n }$

Điều này cho thấy rõ ràng rằng độ phức tạp của hàm này là $O ( 3 ^ { n } )$.
Note: Chúng ta cũng có thể sử dụng các định lý về Subtraction and Conquer cho bài toán này.

Problem-22

Tìm độ phức tạp của hàm đệ quy: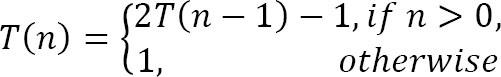

Solution: Chúng ta hãy thử giải quyết function này bằng cách substitution(thay thế):
$T ( n ) = 2 T ( n - 1 ) - 1$
$T ( n ) = 2 ( 2 T ( n - 2 ) - 1 ) - 1 = 2 ^ { 2 } T ( n - 2 ) - 2 - 1$
$T ( n ) = 2 ^ { 2 } ( 2 T ( n - 3 ) - 2 -1 ) = 2 ^ { 3 } T ( n - 4 ) - 2 ^ { 2 } - 2 ^ { 1 } - 2 ^ { 0 }$
$T ( n ) = 2 ^ { n } T ( n - n ) - 2 ^ { n - 1 } - 2 ^ { n - 2 } - 2 ^ { n - 3 } \text { . . . } 2 ^ { 2 } - 2 ^ { 1 } - 2 ^ { 0 }$
$T ( n ) = 2 ^ { n } - 2 ^ { n - 1 } - 2 ^ { n - 2 } - 2 ^ { n - 3 }- \text { . . . } 2 ^ { 2 } - 2 ^ { 1 } - 2 ^ { 0 }$
$T ( n ) = 2 ^ { n } - ( 2 ^ { n } - 1 ) [ n o t e: 2 ^ { n - 1 } + 2 ^ { n - 2 } + \cdots + 2 ^ { 0 } = 2 ^ { n } - 1]$
$T ( n ) = 1$

=> Complexity là $O ( 1 )$.

Problem-23

Xác định running time của function sau:

	public void Funtion(int n) {
		int i = 1, s = 1;
		while(s <= n) {
			i++;
			s = s + i;
			System.out.println("*");
		}
	}

Ta có thể xác định $^ { \prime }s ^ { \prime }$ theo quan hệ $s _ { i } = s _ { i - 1 } + i$ với giá trị của $^ { \prime }i ^ { \prime }$ tăng 1 sau mỗi vòng lặp.
Giá trị chứa trong ‘s’ ở lần lặp thứ i là tổng của các số nguyên dương ‘i’ đầu tiên.
Giả sử k là tổng số lần lặp được thực hiện bởi chương trình, thì vòng lặp while kết thúc nếu:

$$s = 1 + 2 + \ldots + k = \frac { k ( k + 1 ) } { 2 } > n \Rightarrow k = O ( \sqrt { n } )$$

Problem-24

Xác định running time của function sau:

	public void Funtion(int n) {
		int i = 1, count = 0;
		for (i = 0; i*i <= n; i++) {
			count++;
		}
	}

Solution: Trong hàm được đề cập ở trên, vòng lặp sẽ kết thúc, nếu $i ^ { 2 } > n => T ( n ) = O ( \sqrt { n } )$. Tương tự Problem-23

Problem-25

Xác định running time của function sau:

	public void Funtion(int n) {
		int i,j,k, count = 0;
		for(i = n/2; i <= n; i++){
			for(j = n/2; j <= n; j++){
				for(k = n/2; k <= n; k = k*2){
					count++;
				}
			}
		}
	}

Solution: Chúng ta hãy xem lại code, mình sẽ comment chi tiết ở từng vòng lặp

	public void Funtion(int n) {
		int i,j,k, count = 0;
		//Vòng lặp ngoài cùng thực thi n/2 lần
		for(i = n/2; i <= n; i++){
			//Vòng lặp giữa thực thi n/2 lần
			for(j = 1; j + n/2 <= n; j++){
				//Vòng lặp trong cùng thực thi logn lần
				for(k = n/2; k <= n; k = k*2){
					count++;
				}
			}
		}
	}

=> Complexity của function trên là $O ( n ^ { 2 } l o g n )$

Problem-26

Xác định running time của function sau:

	public void Funtion(int n) {
		int i,j,k, count = 0;
		for(i = n/2; i <= n; i++){
			for(j = 1; j <= n; j = 2*j){
				for(k = n/2; k <= n; k = k*2){
					count++;
				}
			}
		}
	}

Solution: Chúng ta hãy xem lại code, mình sẽ comment chi tiết ở từng vòng lặp

	public void Funtion(int n) {
		int i,j,k, count = 0;
        //Vòng lặp ngoài cùng thực thi n/2 lần
		for(i = n/2; i <= n; i++){
            //Vòng lặp giữa thực thi logn lần
			for(j = 1; j <= n; j = 2*j){
                //Vòng lặp trong cùng thực thi logn lần
				for(k = n/2; k <= n; k = k*2){
					count++;
				}
			}
		}
	}

=> Complexity của function trên là $O ( n l o g^ { 2 } n )$

Problem-27

Xác định running time của function sau:

	public void Funtion(int n) {
		if(n == 1) return;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				System.out.println("*");
				break;
			}
		}
	}

Solution: Chúng ta hãy xem lại code, mình sẽ comment chi tiết ở từng vòng lặp

	public void Funtion(int n) {
		//constant time
		if(n == 1) return;
		//Vòng lặp ngoài cùng thực thi n lần
		for (int i = 1; i <= n; i++) {
			//Vòng lặp trong chỉ thực thi 1 lần do lệnh break;
			for (int j = 1; j <= n; j++) {
				System.out.println("*");
				break;
			}
		}
	}

=> Complexity của function trên là $O ( n )$. Mặc dù vòng lặp bên trong có giới hạn là n, nhưng do câu lệnh break nên nó chỉ được thực thi một lần.

Problem-28

Một hàm đệ quy cho thời gian chạy $T ( n )$ của function cho dưới đây. Chứng minh bằng phương pháp lặp rằng $T ( n ) = \Theta ( n ^ { 3 } )$.

	public void Funtion(int n) {
		if(n == 1) return;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				System.out.println("*");
			}
		}
		Funtion(n-3);
	}

Solution: Chúng ta hãy xem lại code, mình sẽ comment chi tiết ở từng vòng lặp

	public void Funtion(int n) {
		//constant time
		if(n == 1) return;
		//Vòng lặp ngoài cùng thực thi n lần
		for (int i = 1; i <= n; i++) {
			//Vòng lặp trong cùng thực thi n lần
			for (int j = 1; j <= n; j++) {
				//constant time
				System.out.println("*");
			}
		}
		Funtion(n-3);
	}

Sự lặp lại đối với mã này rõ ràng là $T ( n ) = T ( n - 3 ) + c n ^ { 2 }$ đối với một số hằng c> 0 vì mỗi lệnh gọi in ra $n^2$ dấu hoa thị và chính nó gọi đệ quy với $n-3$. Sử dụng định lý chính Subtraction and Conquer master theorem, ta được $T ( n ) = \Theta ( n ^ { 3 } )$.

Problem-29

Xác định giới hạn Θ cho hàm sau: $T ( n ) = 2 T ( \frac { n } { 2 } ) + n l o g n$
Solution: Sử dụng Divide and Conquer master theorem, ta được $O ( n l o g ^ { 2 } n )$

Problem-30 (Xem thêm Problem 62)

Xác định giới hạn Θ cho hàm sau: $T ( n ) = T ( \frac { n } { 2 } ) + T ( \frac { n } { 4 } ) + T ( \frac { n } { 8 } ) + n$
Solution: Thay vào phương trình lặp lại, chúng ta nhận được:
$T ( n ) \leq c 1 * \frac { n } { 2 } + c 2 * \frac { n } { 4 } + c 3 * \frac { n } { 8 } + c n \leq k * n$ , với k là 1 constant.
=>$T ( n ) = Θ ( n )$.